Purpose: Puzzles focus on two mathematical ideas.

1. “Expanded notation” using blocks, not writing, as notation: creating two- and three-digit numbers by multiple addition of 1s, 10s and 100s, using only addition.

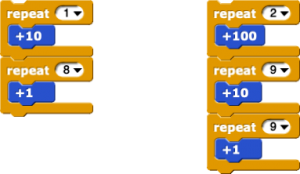
Figure 1: Left, 18 made with 1 ten + 8 ones; Right, 299 made with 2 hundreds + 9 tens + 9 ones

2. Rounding and adjusting: creating two- and three-digit numbers by recognizing and creating nearby roundings to the nearest 10 or 100 and using subtraction to adjust.

Figure 2: Left, 18 rounded to 20, then adjusted by subtracting 2 ones (shown two ways); Right, 299 rounded to 300 and then adjusted by subtracting 1

Children learn by experimenting and seeing the effect of their work. They learn how adding (and subtracting) 1, 10, or 100 affects the value, the written numeral and the spoken number name; they puzzle out how to get particular results; they explore adding 9 by thinking about adding 10 and then adjusting (subtracting one); and they explore multiple additions of 9 by applying the same thinking multiple times; they practice adding 9 mentally with brief and lively oral/aural exercises, and explore doing the same with adding 19 and 99 by using the easier addition and then adjustment.

Work is not “checked” as in tutorial apps and games. Children see the effects their code produces and change it if they like. Children mark “I did it!” on a pdf as they do the puzzles.

Description: Children see Dino, happily announcing that it’s thinking the number 0.

They also have six programming blocks, , , , ,  and , with which to tell Dino what they want it to add or subtract. Dino always reports the new result. If children want Dino to start back with 0, or to start with a different number in mind, they can specify the desired starting place with . It defaults to 0 but the child can change it.

And they have to let them specify specify the number of additions or subtractions to perform (instead of performing them one by one and counting).

Children can choose new explorations, puzzles, and challenges (Figure 3).

 

Some puzzles involve turning a script that does a particular job, like , into a new block, like , that instructs Dino to add or subtract numbers other than 1, 10, and 100. And sometimes they “test Dino” to see if Dino gets the right answer!

Introducing this in class: The very small number of programming blocks and the clear context—familiar symbols on blocks—make it easy to introduce this in less than 10 minutes to 7-year-olds who have had little prior programming experience. Show how to drag a block and how to click; have a child come up to demonstrate another move; show how to type a number other than 0 in the  block (and then click it); have a child show the same; and show how to get a new puzzle. Children do half the demonstrating and can then work independently. They will slip, but they get immediate feedback on what their code does, so they can self-correct.

Teacher notes:

1. We recommend that children have their first mathematical coding experience with the number line microworld, but they can start with this one.
2. Before introducing the computer microworld, this playful, light, brief and lively mental-math warmup sets the stage. NO LONGER THAN ABOUT THREE MINUTES. Gather children on the rug. Tell everyone to “Start with 30. Do you now have a 30 in your head? And you? And you? Everyone? OK, if I say ‘ten more’ you’ll say…. Right! Forty. Mostly, I’ll say ‘ten more’ and you’ll call out what you have in your head, but don’t get ahead of me, because sometimes, I’ll say something different, like ‘one more,’ or ‘ten less.’ Ready?” Then, say a string of ‘ten more’ until children get to 80 or 90 and then ‘ten less’ back to around 50 and then one time ‘one more’ (to 51) and start ‘ten more’ again. Play at a lively pace, not rushing the children, but rushing yourself to pose a new task as soon as they’ve responded. The aim is for them to be comfortable adding and subtracting 10 or 1 starting at any number (e.g., 54, 64, 74, 84, 85, 86, 76, 66, 56…). If children are enjoying the challenge, you can have them add or subtract 100.
   Note: Even for children who are quite able to add or subtract 1, 10, or 100 in their heads, it is very hard for children, at this age, to hold numbers reliably in their heads while switching quickly among those operations, so expect lots of slips. If children give conflicting answers, just check in “what number did we start at?” as if you are, yourself, unsure, and choose one response, right or wrong, to declare as the new starting point.
3. Choose (a) if children have not worked in the number line microworld. Go directly to (b) if children have previously worked in the number line microworld.
   
   1. For children who have not used the number line microworld and are seeing coding for the first time now, compare coding to language. “What languages do we speak in this class?” “We’ll learn a language the computer knows. Here (show the microworld and point to the blocks) are some of its words.” See the Number Line introductory video [link here] for one way to introduce the coding. “Clicking on these ‘words’—we call them blocks—tells the computer what we want Dino to do. We can snap these blocks together like Legos to make a sentence that tells the computer more things to do.”
   2. Children who have used the number line microworld will remember a lot. Just say “Now we’ll teach Dino to add or subtract 1, 10, or 100, like you just did!” Ask a child to drag out one addition (or “plus”) block and show what happens. Ask another child to show how to start Dino back at 0. Ask someone else to show how to start Dino at 34. Ask someone else, what Dino should say if we tell Dino to add 10 to that. (44) Then have someone see if Dino “gets the right answer.”
4. No puzzle in the microworld refers to or uses negative numbers, but children often arrive at them by accident, and with great delight. Children often recognize these and feel excited and proud at finding them; nearly all know what blocks to click to get back to “ordinary numbers,” and many can even predict what number they’ll arrive at. No further discussion is needed at this point.