Purpose: The experience of “zooming in” on the number line allows children to see new numbers between the integers (to one and two decimal places) and to explore adding and subtracting, location, magnitude and distance. Children learn to predict the results of various moves in terms of distance and magnitude on the number line. For example, children come to understand that 3.8 is greater than 3.79. They also experience “crossing over” integers—for example, starting at 3.8 and adding 0.4 lands at 4.2, not 3.12.

Work is not “checked” as in tutorial apps and games. Children see the effects their code produces and change it if they like. Children can mark “I did it!” on a checklist as they do the puzzles.

Description: Children see a number line with the integers of 3, 4 and 5 labeled and the spaces beneath them marked off with positions for nine new numbers creating ten new intervals (tenths) (Figure 1). We name these new numbers by using the starting number of the interval (e.g., 3) and then appending 1 through 9 to distinguish the new numbers (3.1, 3.2, 3.3, … 3.8, 3.9).

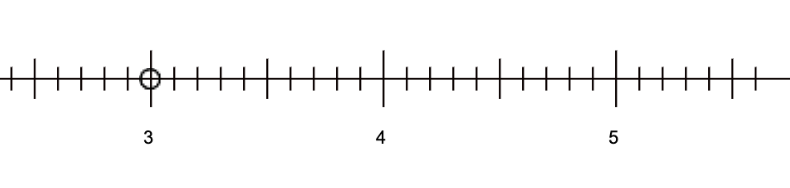
Figure 1: number line divided in tenths

Children then “zoom in” further to create nine new numbers between each of the ones they already know. Again, the new ones are labeled by appending 1 through 9 to the start of the interval (e.g., 3.71, 3.72, 3.73, etc.). Because we have divided tenths into ten parts, these new numbers are indicating hundredths (Figure 2).

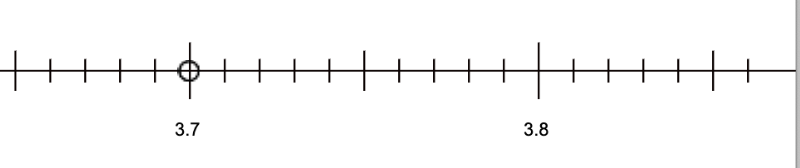
Figure 2: number line “zoomed in” to hundredths

Four blue blocks—   —let them move on the number line by tenths. Each move draws the proper arc and labels the new number. Children can also specify a starting place with the  block. The block defaults to 0 but can be changed by the child as they need.

In later puzzle sets, the four blue blocks change to hundredths— —as students continue to experiment with magnitude and location on the number line. They deepen their understanding of decimals using computer commands to perform experiments on a further “zoomed in” number line.

Children click the gray buttons located below the programming blocks to select new puzzles, and they click the gray buttons below the stage to select new sets of puzzles—tenths, tenths challenge, hundredths, and hundredths challenge (Figure 3). While puzzles are offered in a highly intentional sequence, the microworld does not enforce that sequence, allowing children to customize their path through each puzzle set.

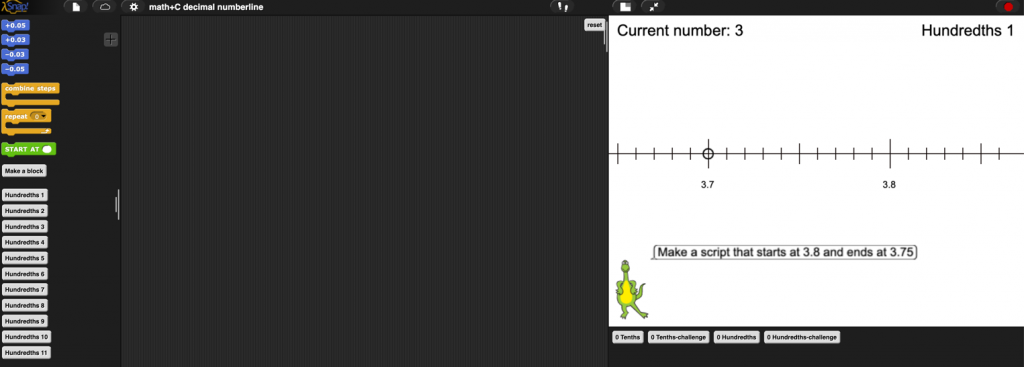
Figure 3: Hundredths puzzle set with hundredths programming blocks

Introducing this in class: The very small number of programming blocks and the clear context—familiar symbols on blocks and a familiar number line image partitioned in tenths—make it possible to introduce this in less than 10 minutes to children who have had little to no prior programming experience. Show how to drag a block and how to click; have a child come up to demonstrate another move; show how to type a number other than 0 in the start at block (and then click it); have a child show how to start at a different place; and show how to get a new puzzle. Children do half the demonstrating and can then work independently.

When the environment transitions to a further “zoomed in” number line in hundredths, have children repeat the demonstrations and ask them what they see that is similar and what is different? Children will learn how the microworld operates, and how the mathematics operates, through experimentation and exploration. Children who have not worked with decimals will need to know how these new symbols are pronounced—“three tenths.”

Teacher notes:

1. For children who are studying decimals but have never used a microworld like this with whole numbers, you may want to give them a bit more experience with the integer number line.
2. For children who have not coded before, compare coding to language. “What languages do we speak in this class?” “We will use and learn a language the computer knows. Here (point to the blocks) are some of its words. When we click them, the computer does what we said. We can snap them together to make a sentence that tells the computer more things to do.”