Finding All the Factors – Elementary Math

Purpose

List factors of a given number

Materials

whiteboard, marker (for individual students)

Overview

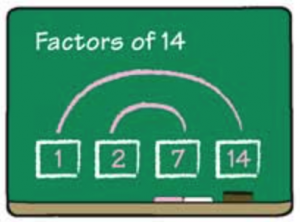factors of 14 Write a number on the board and ask the class to list all of its factors. Encourage students to list factor pairs. As they suggest them, you may choose to record the pairs on the board using a factor diagram organization as pictured here.

Have students find the factors for prime numbers (such as 7 and 19) and composite numbers (such as 14, 15, and 30). After students have found the factors for at least 5 different numbers, ask them to classify the numbers as prime or composite and explain how they know. Students should remember that prime numbers have exactly 2 factors, while composite numbers have more than 2 factors. Student volunteers can also share numbers and ask the class to name factors and classify as either prime or composite.

About the sequence

Part 1 asks students to factor pairs for numbers less than 25 and then classify numbers as either prime or composite. In Part 2, the pace quickens as students continue to name factor pairs for numbers less than 100 and classify each number as prime or composite. The extension explores bigger numbers, their factors and classification.

Part 1

Let’s find factor pairs for the following numbers. After we find the factor pairs, determine whether each number is prime (exactly 2 factors) or composite (more than 2 factors).

Examples:

10 (1 and 10, 2 and 5, composite)
18 (1 and 18, 2 and 9, 6 and 3, composite)
12 (1 and 12, 2 and 6, 3 and 4, composite)
7 (1 and 7, prime)
9 (1 and 9, 3 and 3, composite)

While children are enjoying their building of mastery, feel free to repeat. When children are eager for more, try Part 2 or the extension.

Part 2

I’ll share a number between 0 and 100. Then, we’ll list factor pairs for each number. After all the factor pairs are listed, we’ll classify each number as composite by raising one hand, or as prime by keeping both hands down. Ready, here we go!

Examples:

21 (1 and 21, 3 and 7, composite, hand up)
2 (1 and 2, prime, hands down)
5 (1 and 5, prime, hands down)
45 (1 and 45, 5 and 9, 3 and 15; composite, hand up)
99 (1 and 99, 9 and 11, 3 and 33, composite, hand up)
31 (1 and 31, prime, hands down)
27 (1 and 27, 3 and 9, composite, hands up)
91 (1 and 91, prime, hands down)

As always, when children seem excited for a new challenge, move on.

Extension

Now using your whiteboard and marker, let’s find at least four numbers between 4 and 101 that have at least four sets of factors and make a list of the factors for each number.

Examples:

30 (1 and 30, 2 and 15, 3 and 10, 6 and 5)
40 (1 and 40, 2 and 20, 4 and 10, 5 and 8)
60 (1 and 60, 2 and 30, 3 and 20, 4 and 15, 5 and 12)
80 (1 and 80, 2 and 40, 4 and 20, 5 and 16, 8 and 10)
100 (1 and 100, 2 and 50, 4 and 25, 5 and 20, 10 and 10)