This page describes one silent teaching activity that serves, at the superficial level, to give students useful practice with multiplication facts, but that also builds deeper ideas that both help with fact recall and foreshadow important algebraic ideas. Extensions of this activity give students a mini-research experience finding a surprising and useful pattern, and also an opportunity to develop language, including algebraic language, to describe the pattern.

Finding an exciting pattern: a multiplication activity

Setting the stage, an example of teaching-without-talking (silent teaching)

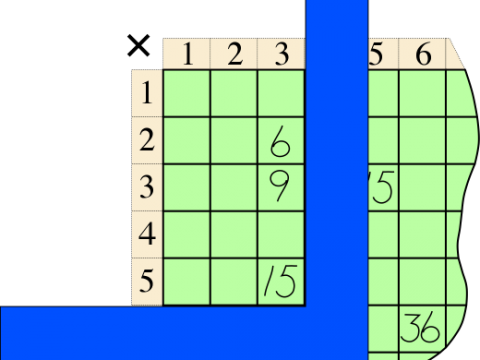
Depending on your class, you might need to call attention to the “start” of this activity because you (the teacher) will not speak a word (silent teaching) during the activity. It will be clear that students may speak, but you’d like them not say anything about any patterns they see, lest they “steal” another student’s opportunity to discover it, too. Then, silently — without explaining anything to the class — draw a segment of a number line, with numbers up through 11. Somewhere nearby but distinctly off the number line, write a small times sign with a circle around it to “set the context” as multiplication. Choose a number that you are sure your students will find easy to square (to multiply by itself), draw two arrows above it, and write the square (the product of that number times itself), like this.

Surround it with two arrows from that number’s nearest neighbors (in this example, 5 and 7). Pause as if to think, and then write their product (35).

Each example of this pattern shows the square of a number (in this example, so far, the squared number was 6, and so the square was 36), directly followed by the product of that number’s ‘nearest neighbors’ (in this case, 5 times 7).

“Search” with your hand, as if deciding what example to give next, and pick a number just far enough so that the arrows won’t overlap your first example. Draw two arrows up from that number, and write the square of that number.

Now the stage is set. Students have enough information for most to guess that you are multiplying, and that the arrows indicate which numbers are being multiplied.

You don’t have to start with these numbers, or remember any special order for the numbers used in this activity. Your choice of examples is up to you. Just choose “medium-challenge” ones — easy enough for all students to do, but not, for example, 2×2 which is both too babyish and also too easily confused with 2+2 because the answers are the same!

Letting students discover

Once again, draw arrows from the nearest neighbors…

…but don’t write in the product. Offer the marker to any volunteer.

The order of examples you give does not matter, but each must follow the same pattern: a square followed by the product of the two nearest neighbors. At first, choose “easy” ones, facts your sure your students will know, so that their attention can be on the evolving pattern. Later, that pattern will help them remember facts they are less sure of.

You might continue like this, extending the number line to the right or left as you please, and drawing the arrows yourself, but each time handing the marker to a student to fill in the numbers.

. . . . . .

. . . . . .

The color change doesn’t mean anything, but helps students visually separate the arrows. You do want the first few examples in the same color so that students pay attention to the numerical pattern and are not distracted by the color (by, for example, thinking it is part of the pattern or some kind of clue). That’s why the first few examples should be reasonably far apart.

Here is how the pattern might look after eleven students have had a turn.

Extending the pattern

When students have caught on to the pattern, find a blank area of the board and silently (still without comment) “extend” the number line this way:

Feel free to use the “…” and not fill in any of the intervening numbers.

Offer the marker, and when a student fills in the 400, you add the two outside arrows (unless the student has already done that!), like this:

Offer the marker and then extend the number line again. As before, you may show only the necessary part of the number line, using “…” to indicate the missing parts.

Then add new arrows and let a student feel brilliant

If you like, do one or two more such extensions. Always make sure that the “middle number” is easy to multiply by itself mentally.

Describing the pattern

Words were deliberately avoided earlier for two reasons. You remain silent so that students are watching, searching, and making their own discoveries, and so that they can “take credit” for anything they learn (because nobody told them!). Also, students must not give the pattern away, because that steals the opportunity from some other student who had not yet made the discovery, but would after one or two more examples.

When students solve these extension problems, they are showing (still without words!) that they’ve found the pattern. After enough eager faces have shown they’ve got it, you can ask children to try describing the pattern. It is astonishingly difficult to get this clear in words! “If you multiply a number times itself, then when you multiply the number just less than it times…” Very cumbersome! But if we abbreviate some of the words, it gets easier.

Let’s start by giving names to these numbers: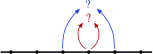

• The first number we pay attention to — the one that we square (see red arrows) — will just be called Number.
• The number to its left — just 1 smaller than “Number” — could be called (Number − 1).
• The number 1 larger than “Number” could be called (Number + 1).

We are comparing two products, and , so now it is much easier to state the rule.

is always 1 less than

Moving toward algebraic shorthand: As adults who have taken algebra, we know more “standard” ways to write these expressions, but young learners do well getting the idea first and the refinements later. To start, use the whole word “Number,” as shown above, to emphasize the communication and meaning, rather than the form.

• After a while, say that writing out the word Number gets tiresome and takes a lot of space, so, let’s find something shorter, a “nickname” for Number. We could nickname it n (for “number”) or c (for “the center number”) or anything else we will all agree on.
• Then, if we’ve used the nickname n, the number just smaller than Number, which we had called (Number − 1), could be nicknamed (n − 1). The number just larger than Number could be nicknamed (n + 1).
• It is helpful to write out the new nickname-style equation below the whole word equation so that students can see that they are basically the same.

is always 1 less than
is always 1 less than 

This is a kind of algebraic pidgin language — a mixture of English words and not-quite-grammatical algebra (the times sign isn’t standard in algebra) — but it is clear. At this stage, this casual mix helps students see that algebraic symbols make mathematical descriptions easier rather than harder. In elementary school, in fact, it may help not to press for grammatical algebra. Children as young as second grade can use symbols like (n + 1) or (b − 8) expressively, to describe patterns they see because the symbols are treated only as abbreviations for normal spoken language, with no special attention, and no discussion of “variables” or even “letters standing for numbers.” (The “n” is just a nickname or abbreviation for “the Number we started with.”)

Young children are excellent language learners. In elementary school, given the opportunity to learn algebra as a communication tool (even as a pidgin language), most children can learn to use these symbols to describe what they already know. But to derive what they do not know will take longer; most will need to be older before they are able to use algebraic symbols in that way.

Checking the pattern by performing the multi-digit multiplication

But have we checked to see whether 49 x 51 really is 2499?! Maybe the pattern holds true for the single-digit facts that we know, but doesn’t actually work for double-digit numbers! This is an opportunity for students to practice double-digit multiplication to check. It is also a nice opportunity for collaborative research. If each student picks just three examples, the class, as a whole, will have checked many examples (let them figure out how many!).

Obviously, there is no way of checking every possible set of three consecutive numbers — there are infinitely many — but a person who is curious looks for “strange” cases to check. So far, we know about single-digit numbers (like 7, 8, 9). Students may have checked cases where the middle number (the number that was squared) is 20 or 30 or 50 or some other multiple of 10 (like 49, 50, 51).

• What about multiples of 10 that are greater than 100?
  

For example, what about 119, 120, 121?
Can they do 120 × 120 in their heads? (Do they recognize the 12 × 12 fact that is camouflaged in this problem? Do they know how to adjust 12 × 12 to get 120 × 120?) From that, what do they predict 119 × 121 will be? Now check, by multiplying, to see if the prediction holds.

• Does the pattern work for sets of three consecutive numbers that don’t include a multiple of 10?

Try, for example, 56, 57, 58?

They’d have to multiply 57 × 57 and check to see if 56 × 58 is exactly 1 less.

• The class might investigate the special cases where the middle number ends in 5.
  

What about 74, 75, 76?

This investigation leads to another pattern while giving useful practice multiplying. (Students will gain insight about this pattern later.)

Understanding why it works

So that we don’t fool ourselves and jump to silly conclusions, we must check some variety of cases. We can’t possibly check all cases, but after a while, we don’t care because we are convinced. We no longer wonder whether it works for all numbers, but we do wonder why it works.

For high-school students who have learned algebra, algebra can help. But algebraic proofs are inappropriate in elementary school, and not always completely “satisfying” even in high school. For fifth graders, dissecting arrays can help them see exactly why this pattern works. That understanding will also show that it must work for any numbers.

We know that 6×4 is one less than 5×5 — that is just a fact we learned — but if we want to know why the “one-less” rule works not only for 4,5,6 but for any three consecutive numbers, we need more than a memorized fact. Let’s start by examining this one specific case — 4,5,6 — to see where that gets us.

We will start with a picture of 5×5. For multiplication, arrays are especially powerful pictures. So, here is a 5-by-5 array: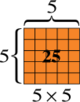

We want to compare 5×5 to 6×4, so we need to find a way to convert the 5×5 picture into a 6×4 picture. Let’s start by slicing off one column:

If we simply remove the column, the picture will be 5×4. If we turn it and place it at the bottom, the picture is “mostly” 6×4 but the new bottom row sticks out one, because the upper part is narrower, by one column, than it used to be.

That arrangement still has 25 tiles in it. If we remove that 1, what’s left is a 6×4 rectangle. 6×4 is truly one less than 5×5.

Though this is just a special case, the way we analyzed it shows that any other special case would have behaved the same way. One column is missing, so when it is turned into a row, it will stick out one.

Further extensions for all students

What students have done so far — along with getting a bit of fact practice — is part of a piece of mathematical research. They have compared the square of a number to the product of the numbers one step away from that number:

Two steps away

A good researcher asks the next reasonable question: “What about two steps away?”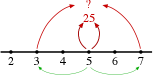

Start the pattern, silently again, with students, and continue only far enough for them to get the idea of what this new exploration is. This time, you can offer the marker to students right away, since the stage has already been set by the earlier activities. Again, start with “easy” facts, like …

You might do three or four examples, perhaps ending like this and then encourage students to do it on their own, trying several more examples.

When they are ready, sketch and hand the marker to someone. Of course, it gets followed by
You might try one or two more, but then offer a new challenge:
If this proves to be too much of a leap, silently offer this hint:

Checking and describing

• Have we checked to see whether the pattern we are following really holds for these bigger numbers? Multiply to check! Have we checked a few “weird” cases? Three-digit numbers? (Everybody do one “weird” three-digit case.)
• How can we describe this new pattern? Again, we can use the nicknames. We are comparing to .

Three and four steps away

The same procedure — silent beginning, some exploration on their own, silent extensions — can be used for researching three and four steps away.

• Each should be its own research project.
• Each should be extended.
• Each should be checked.
• Each should be described.

Before doing five steps away, students should get the chance to reflect back on what they’ve already discovered. Perhaps they can find something in their work that would let them predict the rule for five steps away! Even if they do, of course, they should check that prediction by doing the research in the same way.

Five steps away, and yet another extension

For five steps away, the description of the pattern might look like this: is always 25 more than

or is always 25 less than

The rule for five steps away, by the way, makes it easy to square two-digit numbers that end in 5. Take 35, for example. According to the rule, the product of numbers five steps away should be 25 less than the square of that middle number. So, if 35 is the “middle number,” then the numbers that are five steps away on either side are 30 and 40. That means that 35 × 35 is 25 more than 30 × 40. Aha! 1200 + 25 is the answer!

And now that we know the square of 35, we can easily use our earlier rules about the neighbors of squares to figure out 34 × 36 or 33 × 37.

34 and 36 are one step away from 35, so their product is 1 less than 1225. Similarly, we can multiply 33 × 37 mentally: they are two steps away from 35, so their product is 4 less than 1225. There’s a pattern to find here, too!

Try these:

• 45 × 45
• 48 × 42
• 54 × 56

Understanding why it works

As before we can experiment with arrays.

To understand the pattern for numbers that are two steps away let’s again start with a picture of 5×5:

To compare 5×5 to 7×3, we need to slice off two columns:

Turning both columns and placing them at the bottom gives us an arrangement of 25 tiles (same as it started) that is now 7 rows tall 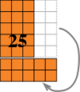, and mostly 3 columns wide, but again with a part that sticks out. Each bottom row sticks out two, because the top of the figure is narrower by two columns than it started out. So, the sticking out part is 2 × 2.

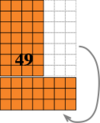
If we remove that 2 × 2 square the part that is left is a 7×3 rectangle. 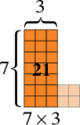7×3 is truly four less than 5×5.

We can dissect other starting squares to get the “feel” of it but, as before, we begin to see, even in this one case, why any other special case would have behaved the same way. Two columns are missing, so when they are turned into rows, each one sticks out two, a total of 2×2 squares extra.

And for three steps away (and so on), we can perform the experiment again.

….. ….. …..  

An astonishing feat of mental multiplication for any eager child

It takes very little practice, once one has discovered the patterns, to do this trick.

• “Magician” (child), to audience: Give me a two digit number.
• Audience member: OK, 53.
• “Magician”: Thinks: the nearest multiple of 10 is 50. That’s three steps away, so I’ll pick a number three steps away on the other side of 50. OK, and I pick 47. While writing “53 × 47” for all to see, the child thinks: 50 × 50 = 2500; subtract 9 (that is 3 × 3 for the three steps away), which I can get by subtracting 10 and then adding 1 back. 2500 – 9 = 2491. Finishes writing the sentence “53 × 47 = 2491.” And 53 × 47 is 2491. Anybody want to check? How about another two digit number? Any one at all!

Learning a trick is not important. But learning to feel this comfortable with numbers, realizing how much one can do, is important.

Asher, a particularly bright and eager child who knew his multiplication facts as he had just turned eight and was entering third grade, delighted in multiplying numbers that were twelve steps away from a number he could easily square in his head. For example, to multiply 38 × 62, he thought 50 × 50 is 2500, and subtracted 144 (that is, 12 × 12) from that, piece by piece, thinking 2500 (minus 100) 2400 (minus 40) 2360 (minus 4) 2356.

Understanding why again

The logic is the same, but it is worth seeing again. The “magician” thought 50×50 first:

The magician then thought “subtract 3×3” and confidently concluded that 2500 − 9 was the same as 53×47. But the remaining shape is not a rectangle, so it doesn’t help us see that it contains 53×47 unit squares.

So, let’s fix it! Slice off the incomplete 3×47 column and then fit it at the bottom

This is 47 units wide and 53 units tall (or 47 columns and 53 rows, or 53 rows with 47 tiles in each row). So this is certainly a picture of 53×47, and working backwards we can see, therefore, that must be, too.

Extensions for top students

Negative numbers

Even young children find the idea of negative numbers fascinating, but it takes a variety of separate experiences with negative numbers before arithmetic with them, especially multiplication with them, “feels intuitive” rather than just rulebound. Here is one (of many) experiments that help to make multiplication of negative numbers feel natural.

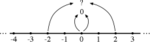
• Try Students know what 1 × 1 is, and also know (from the pattern) that the product of the neighbors that are two steps away (-1 and 3) must be 4 less than 1 × 1. So, counting four steps backward from 1 × 1 = 1, the pattern claims that -1 × 3 is -3. That makes a kind of sense: -3 seems to be “three times as ‘much'” as -1.

• Try Again, we start with what we know: 0 × 0 = 0, and the pattern says that -2 × 2 should be four less than that, or -4. Again, this seems to make sense: the multiplication by 2 makes -4 twice as much debt (or twice as far from zero in that direction, or whatever image helps most) as -2.

• Try Here, we can’t start with the “middle” number, because we don’t yet have any reason to know what negative times negative should be. But we can multiply the two-step-away neighbors! Anything we multiply by 1 is itself! So -3 × 1 is -3. That is supposed to be 4 less than -1 × -1. If the pattern holds, then -1 × -1 must be 1.

• Similarly, try 0 × -4. Because we know that anything times 0 is 0, and because the “middle” number is two steps away from each end, we can figure out that -2 × -2 = 4. Starting from that, and moving just one step away, we get the product -3 × -1, which must be one less than -2 × -2, and so -3 × -1 = 3. This is not an explanation of why negative times negative is positive, but it does add new experience that builds an intuitive sense for such a conclusion.

Intuition doesn’t develop instantly, but it does develop. Experiences like this (and see negative numbers for more) help students develop genuine intuition, so that arithmetic with negative numbers doesn’t feel like following an arbitrary set of incomprehensible rules.

Searching for new patterns

All of the explorations above involved either (1) starting with a number, squaring it, and comparing that result to the product of numbers that differed from it (on both sides) by some fixed quantity or (2) starting with two numbers whose difference was even, and comparing their product to the square of their mean.

There is one other possibility: comparing the product of consecutive numbers (numbers that differ by 1) with the product of their neighbors some fixed distance to the right or left.

If the neighbors are one step away, the situation looks like this, .

If they are two steps away, it looks like this, .

Because numbers like 70 and 71 are easy to multiply — 70² + 70 — the pattern allows one to multiply 68 × 73 in one’s head:

After exploring one step and two steps (as above), we may explore three and four and more steps away, looking for a generalization.

Asher’s theorem: a case of beautiful mathematical intuition After just a bit of experimentation, the rule for “one step away” seems to be “subtract 2” and, for “two steps away,” seems to be “subtract 6.” An attempt to generalize from just those two observations could lead to many conjectures. Two tempting (but wrong) ones are:

• Start at “subtract 2” for “one step away.” Each further step away would require subtracting 4 more (i.e., 2, 6, 10, 14…).
• To decide what to subtract, double the nth odd number where n is the number of steps away. So, for 1 step away, double the first odd number (1), and for two steps away, double the second odd number (3), and so on (i.e., 2, 6, 10, 14, …, resulting in the same pattern).

Of course, generalizing from only two cases is likely to lead to wrong conjectures, but it is quite natural to have hunches even before one has checked things out.

Asher was not yet nine years old when he was exploring this multiplication pattern. After seeing just the 2 and 6, he had a hunch, but a very different and much more sophisticated one than the ones given above. He had already extended the difference-of-squares idea until he could perform multiplications like 32 × 68 — that is (50 – 18)(50 + 18) — fairly easily in his head. The number to subtract was always the “number of steps away” squared. In this new experiment, we are not squaring, but multiplying consecutive numbers, and Asher’s keen intuition led him to conjecture that the 2 and 6 were derived that way, too: 1 × 2, and 2 × 3. He therefore predicted that the rule for “three steps away” should be “subtract 3 × 4.” He checked it by comparing 4 × 5 (a pair of adjacent numbers) with 1 × 8 (the numbers three steps below and above the original pair), and checked “four steps above and below” just to verify. These numbers, 1 × 2, 2 × 3, 3 × 4, 4 × 5, 5 × 6, …, are 2, 6, 12, 20, 30, …, a sequence that is related to the triangular numbers (1, 3, 6, 10, 15, …) by doubling.

It is just icing on the cake to mention that Asher made this discovery and conjecture in a situation where there was nothing to write on or write with: no calculator, no paper, no pencils. The numbers, the computations, and the results all had to be held mentally. He had met the original problem — difference of squares — the same way. Holding up three fingers (and later, five) he was comparing the square of the number at the middle finger with the square of the two numbers next to it: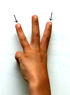 . This new experiment was introduced by putting up four fingers, assigning four consecutive numbers to them (I think we started with 5, 6, 7, 8) and comparing the product of these (6 × 7 = 42) with the product of these 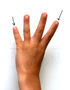(5 × 8 = 40).

What is the purpose of this activity?

Why do it?

It serves pedagogical purposes:

• It gives fact-practice in a context that keeps students alert (and so they get the practice because they are not sleeping through it).
• It gives some two-digit multiplication practice.
• The pattern helps students remember certain facts. For example, many students find 9×7 harder than 8×8. This pattern relates the two, so if you know one, you know the other.
• It gives students a chance to discover something on their own, realize how much they can do, and feel smart. If they learn the pattern well, they can do “amazing feats” of computation that let them feel even smarter! Nobody — no corporation and no person — puts effort into a venture they don’t believe will succeed, and so people who feel that they are not smart in math are often less motivated to do the work that could make them smart, because they don’t expect success. Students who need fact-practice the most are often the ones who feel the least smart in math. Seeing how much they can do helps them put in the extra work that it will take to become more proficient.

It also serves mathematical purposes:

• To multiply 47 × 53 using this pattern, we must focus, and expand our ability to hold several things in mind at once. We must
  • think “ah, each is three steps away from 50,”
  • perform 50 × 50,
  • hold that answer in mind while we recall the rest of the rule (“three steps away, so subtract nine”)
  • perform the mental subtraction.
• It gives experience with some aspects of mathematical research: checking special cases; generalizing (extending the pattern in several ways); describing the generalization.
• It foreshadows some important ideas in algebra.

What is not important?

We don’t care whether students can multiply 47 × 53 (or any other pair of two-digit numbers) in their heads. That is a nice bonus, if students get good at it, and the students love it because it makes them feel smart, but being able to multiply certain pairs of numbers mentally is not the goal.

Remembering the “rule” for each case — one step away, two steps away, and so on — is not the goal.

This is not a new piece of “content” to learn.

But knowing the facts — for which this gives good practice — and being able to apply them even when they are “camouflaged” by multiplication by 10 (e.g., 60 × 60 or 120 × 120) are important. And learning to keep several things in mind at once — finding a product like 60 × 60 and subtracting 4 from it, all mentally — is important. And learning how to investigate systematically (check larger numbers and other special cases) and how to extend an investigation (look two steps out, then three, and then four, see if there’s a way of predicting what five steps out might be, and then checking that, too) is important. And learning a way of describing patterns is important. And if students really get good at the pattern, they can do so many “astonishing” multiplications in their head that they feel brilliant, and feeling brilliant is important, too!

Why silent teaching?

As in all silent teaching, the teacher’s silence both rivets attention — there is nothing to listen to, so one must watch — and also lets the student “take credit” (feel smart) for whatever discovery the student makes, because nobody explained anything! Classroom silence also lets all students have a fair shot at making the discovery. A person who does not see the pattern instantly keeps getting more data as new examples are given, but nobody steals the chance to make the discovery, because nobody explains what they’ve noticed.