MP7 Look for and make use of structure
Mathematical Practice Standard #7
Mathematically proficient students look closely to discern a pattern or structure. Young students, for example, might notice that three and seven more is the same amount as seven and three more, or they may sort a collection of shapes according to how many sides the shapes have. Later, students will see 7 × 8 equals the well-remembered 7 × 5 + 7 × 3, in preparation for learning about the distributive property…. They also can step back for an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects…. —CCSS
The standard in elementary school
Children naturally seek and make use of structure. It is one of the reasons why young children may say “foots” or “policemans,” which they have never heard from adults, instead of feet or policemen, which they do hear. They induce a structure for plurals from the vast quantity of words they learn and make use of that structure even where it does not apply.
Mathematics has far more consistent structure than our language, but too often it is taught in ways that don’t make that structure easily apparent. If, for example, students’ first encounter with the addition of same-denominator fractions drew on their well-established spoken structure for adding the counts of things—two sheep plus three sheep makes five sheep, two hundred plus three hundred makes five hundred, and two wugs plus three wugs makes five wugs, no matter what a wug might be—then they would already be sure that two eighths plus three eighths makes five eighths. Instead, they often first encounter the addition of fractions in writing, as 2/8 + 3/8, and they therefore invoke a different pattern they’ve learned—add everything in sight—resulting in the incorrect and nonsensical 5/16. Kindergarteners who have no real idea how big “hundred” or “thousand” are (though they’ve heard the words) are completely comfortable, amused, and proud to add such big numbers as “two thousand plus two thousand” when the numbers are spoken, even though children a year older might have had no idea how to do “2000 + 3000” presented on paper.
This CCSS standard refers to students recognizing that “7 × 8 equals the well-remembered 7 × 5 + 7 × 3.” Array pictures help (see MP standard 5, “Use appropriate tools strategically”), but so does students’ linguistic knowledge, if the connection is made. The written symbols 5×7 + 3×7 = 8×7 are very compact, but the meaning they condense into just eleven characters is something that students understood well even before they learned multiplication. Before they have any idea what a collection of sevens is, they know that five of them plus three of them equals eight of them. It’s just five wugs plus three wugs again.
“Standard arithmetic” can be taught with or without attention to pattern. The CCSS acknowledges that students do need to know arithmetic facts, but random-order fact drills rely on memory alone, where patterned practice can develop a sense for structure as well. Learning to add 8 to anything—not just to single digit numbers—by thinking of it as adding 10 and subtracting 2 can develop just as fast recall of the facts as random-order practice, but it also allows students quickly to generalize and add 18 or 28 to anything mentally. The structure is a general one, not just a set of memorized facts, so students can use it to add 19 or 39, or 21 or 41, to anything, too. With a bit of adjustment, they can use the same thinking to subtract mentally. This is, of course, exactly the way we hope students will mentally perform 350 – 99.
Structure allows sensible definition of odd and even: pairs with or without something left over.
In elementary school, attention to structure also includes the ability to defer evaluation for certain kinds of tasks. For example, when presented with 7 + 5 7 + 4 and asked to fill in <, =, or > to compare the two expressions, second graders are often drawn—and may even be explicitly told—to perform the calculations first. But this is a situation in which we want the students’ attention on the structure, ♣ + 5 ♣ + 4 or even  + 5
+ 5  + 4, rather than on the arithmetic. Without any reference to symbols “standing for” numbers, which might well be distracting or even confusing to second graders, they readily see that
+ 4, rather than on the arithmetic. Without any reference to symbols “standing for” numbers, which might well be distracting or even confusing to second graders, they readily see that  + 5
+ 5  + 4 if the same number is under each hand. This same skill of deferring evaluation—putting off calculation until one sees the overall structure—helps students notice that they don’t have to find common denominators for 1
+ 4 if the same number is under each hand. This same skill of deferring evaluation—putting off calculation until one sees the overall structure—helps students notice that they don’t have to find common denominators for 1![]() –
– ![]() + 3 +
+ 3 + ![]() –
– ![]() but can simply rearrange the terms to make such a trivial computation that they can do it in their heads. When students begin to solve algebraic equations, the same idea will help them notice that 3(5x – 4) + 2 = 20 can be treated as “something plus 2 equals 20” and conclude, using common sense and not just “rules,” that 3(5x – 4) = 18.
but can simply rearrange the terms to make such a trivial computation that they can do it in their heads. When students begin to solve algebraic equations, the same idea will help them notice that 3(5x – 4) + 2 = 20 can be treated as “something plus 2 equals 20” and conclude, using common sense and not just “rules,” that 3(5x – 4) = 18.
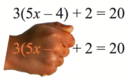
From such reasoning, they can learn to derive rules that make sense.
