Mobile puzzles are pictorial representations of systems of equations; each beam that balances two sets of objects (representing variables as unknown “weights”) represents an equation. Children bring intuitive ideas to these puzzles—a set of “common sense” strategies for solving them—which, over time, translate naturally into the “standard moves” of algebra for solving equations and systems of equations. The mathematical content includes variable, evaluation, substitution, solving equations and systems of linear equations.

Explicit connection with algebraic notation can easily be made when that is appropriate, but it is valuable to build up informal experience with puzzles of this kind over time before making the formal connection.

Nature

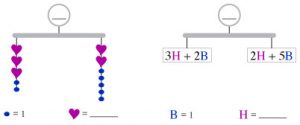
Students can solve the mobile shown here in many ways. They might reason, for example, that since the entire mobile weighs 48, the left side of it… 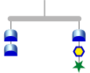must be 24, and so the left side of that — the two blue thingos — must be 12. So each blue thingo must be 6.

Another branch of the mobile  shows that three stars exactly balance a blue thingo, so each star must be 2.

To figure out the hexagon, a student might look again at and see that the hexagon and star together exactly balance a blue thingo: ___ + 2 = 6.

Alternatively, a student might look at the right side of the mobile 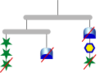and figure out that the hexagon exactly balances two stars.

There are other ways to approach the problem, of course, all requiring only a “common sense” logic. To see that “the hexagon and star together exactly balance a blue thingo,” we might just have “ignored” the extra blue thingo on both sides of that branch of the mobile. In algebra class, we might have called that “subtracting a blue thingo on both sides of the equation,” but we can see the logic of it right here, without any rules. Similarly, seeing that “the hexagon exactly balances two stars” might be described in class as “crossing out” equals from both sides of the balance. It is perfectly obvious here why it works.

By solving puzzles of this kind, students build experience with a variety of logical moves — common sense replacements — that underlie the algebraic moves that they can sometimes see as arbitrary “rules.”