Area formulas

Students who have the informal notion that area is the “amount of 2-D ‘stuff'” contained inside a region can invent for themselves most of the formulas that they are often asked merely to memorize. Each formula they reinvent helps strengthen their understanding (and memory) for the other formulas they know. (See also surface area.)

Area of rectangles

By choosing a square as the unit of area, we get an intuitive idea about the area of rectangles. If we decide that the area of this square is 1, then a rectangle that is 7 times as long would have 7 × 1 as its area.

A rectangle that is twice the height of would have twice its area, so the area of is 2 × 7 units of area. We can count the two rows of seven squares. Similarly, has 3 rows of 7 squares (or 7 columns of 3 squares), for a total of 7 × 3 squares, so its area is 21 square units.

The number of squares in one row is the length of the rectangle. The number of rows is the height of the rectangle. So the area is length × height.

Because a rectangle can be drawn at a slant, “height” is defined to mean “the direction perpendicular to the base,” and “base” is defined to be, well, whatever side you choose it to be.

That works for counting numbers. It even works for fractions. 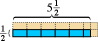The blue rectangle shown here measures one-half length-unit high by five and one-half length-units wide. If we choose the corresponding square as our area-unit, we see that the blue rectangle contains five half-units of area and one quarter-unit of area, or a total of two and three-quarter units of area. (The pink parts show the completion of each square area-unit.)

To include all numbers, we define the area of a rectangle to be base × height (where “base” and “height” mean the lengths of those sides, measured in the same units).

Area of parallelograms

Getting the idea

We can figure out a formula for the area of a parallelogram by dissecting the parallelogram and rearranging the parts to make a rectangle. Because the parallelogram and rectangle are composed of the same parts, they necessarily have the same area. (See the definition of area for more about why those areas are the same.)

We can see that they also have exactly the same base length (blue) and exactly the same height (green). Because base × height gives the area of the rectangle, we can use the same measurements on the parallelogram to compute its area: base × height. (As before, “height” is measured perpendicular to the base, and “base” is whichever side you chose first. See parallelogram.)

The cut shown above makes it easy to see that the base length is unchanged. In fact, the perpendicular cut can be made anywhere along the base.

Shoring up the holes

Intuition and proof

This dissection gives an intuitive understanding of the area formula for a parallelogram, a reason that it should be what it is. But we have not questioned whether the dissection really “works.” That is, when we cut the parallelogram and rearrange its parts, we expect to get and the result certainly looks like that. But appearances can be deceptive. What assures us that when we move that triangle, the result is a rectangle? What if it is more like (though less exaggerated)? If the result is not always a perfect rectangle, we can not use our knowledge of the rectangle’s area formula to develop a formula for the parallelogram. In high school, students will be able to prove that the two parts of the parallelogram, when reassembled properly, do make a rectangle. In grades K-8, for the most part, students must rely on the visual experiment and get an intuitive feel. Learn more about why these dissections work.

What if we pick the short side to be the base?

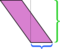
We are free to choose any side as the base; “height” is defined to be measured perpendicular to the side we choose as the base. If we take the short side (blue) as the base, the dissection shown above isn’t as convincing. Cutting along that altitude and rearranging the parts leaves a mess:

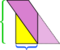
In this particular example, we can salvage the mess by making one more cut, 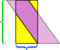but what if the parallelogram were even longer and skinnier?

It turns out that any parallelogram, no matter how long and skinny, can be dissected in this way so that the parts — perhaps many of them — can be rearranged into a rectangle. But it takes more work to show that this can always be done. We need another idea.

A slightly different dissection idea makes life much easier in this case. (On your own, you can show that it works in the original case, too.)

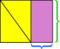
• Enclose the parallelogram in a rectangle.
• The two parts of the rectangle that are not inside the parallelogram are congruent triangles.
• Slide one of these triangles toward the other until they meet to form a rectangle. Because the total area of the outside rectangle has not changed (it is the same rectangle as before) and the yellow area has not changed (the pieces just moved around), the difference between them — the purple areas — must be the same. As before, we can also see that the dimensions of the rectangular purple area are the base and height of the original parallelogram.

Intuition and proof, reprise: Again, the dissection provides the essential insight, but it takes a bit more work to assure that the two yellow triangles, which certainly look as though they fit together to make a rectangle, really do fit precisely, and not just almost.

Why is it important to be so careful?

When we build other area formulas (below), we will want to use our how to find the area of a parallelogram, and so we want to be able to rely on the rule we’ve found. We can be sure that rearranging parts doesn’t change the area: that is, after all, how we define area. But we must also be sure that the parts fit together the way we claim they do, or we can’t rely on the measurements we’ve made. And we must be sure that the base × height rule does not depend on a lucky choice of base.

In most curricula, students don’t have a systematic enough base of geometric knowledge prior to grade 8 to make sound proofs that these dissections work. But the intuitive understanding is enough to explain and justify the formulas, and a good grounding for later geometric study.

Area of triangle

Knowing how to find the area of a parallelogram helps us find the area of a triangle.

Dissecting the triangle

We can dissect the triangle into two parts — one of them a triangle, and one of them a trapezoid — by slicing it parallel to the base. If we cut the height exactly in half with that slice, the two parts fit together to make a parallelogram with the same base but half the height.

So base × half-height gives the area of the triangle. A similar dissection shows half-base × height. Either of them reduces to bh.

Doubling the triangle and then halving the resulting area

Another way of thinking: two copies of the triangle make a parallelogram with the same base and same height as the triangle.

The parallelogram’s area is base × height, but that is twice the area of the triangle, so the triangle’s area is  of base × height, as we saw with the dissection method.

(As always, pick a “base” and measure the height perpendicular to that base, from the base to the opposite vertex.)

Area of trapezoid

Doubling the trapezoid and then halving the resulting area

As was true with the triangle, two copies of a trapezoid can be fit together to make a parallelogram.

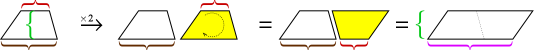
The height of the parallelogram is the same as the height of the trapezoid, but its base is the sum of the two bases of the trapezoid. So the parallelogram’s area is height × (base1 + base2). But that area is two trapezoids, so we need to cut it in half to get the area of the trapezoid.

Dissecting the trapezoid

We could also dissect the trapezoid the way we dissected the triangle, with a single slice cutting its height in half. The two parts fit together to make a parallelogram whose base is the sum of the two bases of the trapezoid, but whose height is half the height of the trapezoid.

In the case of the trapezoid, the bases cannot be chosen at will. The two parallel sides are the bases, and height, as always, is the perpendicular distance from one base to the opposite.

The area of this parallelogram is its height (half-height of the trapezoid) times its base (sum of the bases of the trapezoid), so its area is half-height × (base1 + base2). Because the parallelogram is made from exactly the same “stuff” as the trapezoid, that’s the area of the trapezoid, too.

Either way, the area of the trapezoid is  × height × (base1 + base2).

Area of other special quadrilaterals

Area of rhombus

The area of a rhombus can be found by cutting and rearranging the pieces to form a parallelogram. This can be done several ways:

1. Cut across the shorter diagonal (a) to form two congruent triangles. Move the lower half of the triangle next to the upper half to form a parallelogram. The shorter diagonal (a) becomes the base of the parallelogram, and half the longer diagonal (b) becomes the height of the parallelogram. Thus, the area of the rhombus is a * b or the product of the diagonals, which is the standard formula for rhombus.
2. Another similar way is to cut the rhombus into four congruent triangles and rearranging them into a rectangle with the shorter diagonal as the base and half the longer diagonal as the height.
3. After cutting the rhombus into two congruent triangles, we can calculate the area of one of the triangle, which is * base (a) * height (b) = 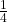ab. Then multiply by two since there are two of them: 2 * 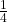ab = ab.

Area of kite

The area of a kite can be found similar to the area of a rhombus. Cutting across the longer diagonal yields two congruent triangles. If we rearrange them, we can form a parallelogram with the longer diagonal (b) as base and half the shorter diagonal (a) as the height. So, the area becomes b * a = ab. A more complicated approach involves a bit of algebra. Cut the kite across the shorter diagonal to form two triangles with the shorter diagonal (a) as the base. Thus the area of the first triangle is a * squiggly, where squiggly is the height. The area of the second triangle is a * (b – squiggly), where (b – squiggly) is the remaining part of the longer diagonal. The total area thus becomes ( a * squiggly) + ( a * (b – squiggly)). Factoring out a, we have a (squiggly + b – squiggly) = ab.

Well, what do you know. Basically, you only need to know the formula for the area of a parallelogram and then derive the formula for the others.