Shape: Quadrilateral
Quadrilateral
A quadrilateral is a polygon that has exactly four sides. (This also means that a quadrilateral has exactly four vertices, and exactly four angles.)
Meaning
A quadrilateral is a polygon that has exactly four sides. (This also means that a quadrilateral has exactly four vertices, and exactly four angles.)
Some examples of quadrilaterals:

Discussions of 2-D shapes sometimes refer only to the boundary (the line segments that form the edges of the figure) or to the interior as well. When we talk about “dissecting” a parallelogram and rearranging the parts to form a rectangle in order to determine the area of the parallelogram, we are clearly referring to the edges and the interior. The usual definitions of polygons, however, refer only to the line segments that form the edges of the polygon. Most of the time, context will make clear what you mean, but you should remain aware that in some cases you may need to clarify.
Elementary school curricula typically have children learn the names of special subsets of quadrilaterals with particular features. Here we list the special names. See the articles on each type for their definitions and special properties.
- trapezoids (A and J are “typical” examples, but all parallelograms also fit the definition of trapezoids);
- parallelograms (E is the “typical” example, but all rectangles and rhombuses also fit the definition of parallelograms);
- rectangles (F is the “typical” example, but all squares also fit the definition of rectangles);
- rhombuses (C and D are the “typical” examples, but all squares also fit the definition of rhombuses);
- squares (B), the most special of them all.
Some K-8 curricula also include
- kites (G and, in some definitions H).
What’s in a word?
quadri- (four) + -lateral (side) means “four-sided.”
Compare quadri- to Spanish cuatro. Lateral means “side” (think of football, for example).
Classification
Just as triangles and quadrilaterals are special types of polygons, there are many subclasses of quadrilaterals.
Like all polygons that have more than three sides, quadrilaterals can be convex like these  ,
,  ,
,  ,
,  or concave like these
or concave like these  ,
,  .
.
Quadrilaterals can be classified by whether or not their sides, angles, diagonals, or vertices have special properties. The classification schemes taught in elementary school involve the number of pairs of parallel sides, and the congruence of sides, and whether or not all the angles are right angles (all angles are congruent).
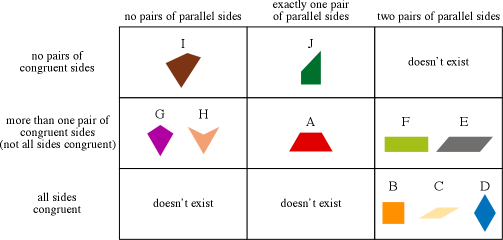
The names of many of these special quadrilaterals are also typically part of the elementary curriculum, though little else about the properties of these figures may be studied until high school. Elementary school typically has children learn the names of
- trapezoids (A and J are “typical” examples, but all parallelograms also fit the definition of trapezoids);
- parallelograms (E is the “typical” example, but all rectangles and rhombuses also fit the definition of parallelograms);
- rectangles (F is the “typical” example, but all squares also fit the definition of rectangles);
- rhombuses (C and D are the “typical” examples, but all squares also fit the definition of rhombuses);
- squares (B), the most special of them all; and sometimes
- kites (G and some include H).
The square is also the name of the regular quadrilateral — one in which all sides are congruent and all angles are congruent.
Though the names that are given to individual figures does not change, the way that they are grouped may depend on the characteristics used to sort them. In the classification scheme shown above, parallelograms (B, C, D, E, and F) have a place of their own (the right hand column), and even rhombuses (B, C, D) have a place (the bottom row), but rectangles (F and B) aren’t distinguished from the others. In the classification scheme below, rectangles (F and B) have the right hand column to themselves, but parallelograms are not grouped in a way that excludes A, which is not a parallelogram.

Children in primary grades often find it hard to assign anything (geometrical or otherwise) simultaneously to two categories.[1] Casual language also treats shape-names as “exclusive” rather than “inclusive.” Thus, casual language treats square and rectangle as distinct, rather than treating square as a special kind of rectangle, as mathematics does. Similarly, students tend to treat rectangles and parallelograms as disjoint classes, rather than seeing a rectangle as a special type of parallelograms.
- Given 6 toy horses and 4 toy cows, and asked whether there are more horses or more animals, very young children often answer “more horses” because in classifying the toys as “horses,” they, for that moment, exclude them as “animals,” even though, if separately asked whether horses are animals, they will say yes.
Another possible way to classify quadrilaterals is by examining their diagonals. This may be accessible for middle grade students who have learned about perpendicular lines and bisectors.
| Diagonals | Perpendicular | Not Perpendicular | ||
|---|---|---|---|---|
| Bisector | Not Bisector | Bisector | Not Bisector | |
| Congruent | Square | Special Kite | Rectangle | Isosceles Trapezoid |
| Not Congruent | Rhombus | Kite | Parallelogram | Quadrilateral |
Mathematical background
Properties
In addition to being four-sided polygons, all quadrilaterals share some additional properties.
Angles in a quadrilateral
The sum of the interior angles in a quadrilateral is 360°. Students who know the analogous result for triangles can convince themselves of this by cutting a quadrilateral into two triangles by drawing a diagonal: each triangle contains 180° of angle measure, so the two triangles contain 360°.
Children can also experiment with this idea by
- coloring or labeling the corners of a quadrilateral
 ,
, - cutting the corners off
 …
…  , and
, and - fitting the colored vertices together to show that they all fit snugly around a point.
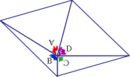
Tesselation: The fact that the four vertices fit snugly around a single point allows us to arrange four copies of a quadrilateral around a point. Regardless of the quadrilateral one starts with, four copies of it can be arranged to fit snugly around a single point.

Multiple copies of that foursome will tile the plane.

Even if one starts with a concave quadrilateral like this  , one can group four identical copies of them snugly around a point
, one can group four identical copies of them snugly around a point  , and can tile the entire plane with multiple copies.
, and can tile the entire plane with multiple copies.
Special topics (rarely in elementary or middle school)
Cyclic quadrilaterals: For some quadrilaterals, it is possible to pass a single circle through all four of its vertices. These special cases, called cyclic quadrilaterals, include rectangles (and therefore squares) and isosceles trapezoids, but also other shapes that have no special name of their own. Cyclic quadrilaterals have the special property that the sum of their opposite angles is a straight angle, or 180 degrees. The implication works in the other direction, too: any quadrilateral whose opposite angles add up to 180 degrees is a cyclic quadrilateral.

When the quadrilateral and the circle passing through its vertices are both shown, the quadrilateral is said to be inscribed within the circle and the circle is said to be circumscribed about the quadrilateral.


Parallelograms that are not also rectangles cannot be inscribed in a circle: they are not cyclic quadrilaterals. A circle that passes through three of the vertices is either too large to pass through the fourth (blue circle at the left) or too small to pass through the fourth (red circle at the right).
In addition to circumscribing circles around a quadrilateral (drawing circles around a quadrilateral, touching each vertex), it is sometimes possible to inscribe a circle (draw a circle within a quadrilateral so that each side of the quadrilateral is tangent to the circle). This group of quadrilaterals has no special name of its own, but includes kites, rhombuses, and squares along with other quadrilaterals that have no particular name.
Investigations: When investigating special quadrilaterals and their properties, students find many ways to distinguish quadrilaterals. Some productive explorations ask students to look for special properties of angles (congruent or supplementary), sides (parallel, perpendicular, or congruent), and diagonals (perpendicular, bisecting, or congruent).
