The author of this post, Dr. E. Paul Goldenberg, has over 40 years of experience in K–12 mathematics curriculum development, research, and professional development. In this post, he shares a story about a surprising discovery he made while observing Emma and challenges us with a question: “How can we run a school in a way that gives teachers the time and support to watch and listen actively and to recognize, understand, and help children build on the underlying mathematical ideas?”

Emma combines the charm of a kindergartener with the caricature of a schoolmarm. When she’s the leader at calendar time in class, she’s likely enough to begin with “Now class, what number comes next?” And when Emma was making an elaborate design with pattern blocks, periodically narrating what she was doing, she announced at the end, “And now it’s done. Thank you for watching so patiently.”

Near the end of the year, each child in this particular kindergarten created a personal booklet to show what he or she had learned about adding and subtracting. Each page had a different caption, like “I can add two numbers to make 10” or “I can subtract a number from 10” or “I can add 10 to a number I choose.” Most of the pages focused on making or using 10; all of the pages allowed some personal choice. Children were generally asked both to write an equation and to draw a simple picture to illustrate the meaning of the operation.

These children were used to working with large numbers and quite proud of it, so most children chose “big” numbers for their booklet pages wherever they could. To illustrate, dots or tally marks would have been enough, but they almost all drew collections of flowers or bunnies or smiley-faced people one at a time, counting as they went, and re-counting after a few more pictures to make sure they had the right number. A few of them arranged their pictures in rows or groups that made the counting easier, but most of them just squeezed pictures onto the page wherever they would fit.

One way to understand the Mathematical Practice of looking for and making use of structure (MP8) is to see the kinds of structures young children build. Even the youngest children build and use structure in their mathematical thinking. As teachers, we nurture this by creating space and time for them to investigate ideas and by being attentive and curious about their thinking. What we, as teachers, pay attention to shapes what children pay attention to. Our genuine interest in a child’s mathematical thinking helps make that thinking feel important to the child.

On one of the end-of-year-booklet pages, Emma chose 30 as her starting number. She carefully explained to me—Emma always explains things, often a bit professorially, to anyone willing to listen—that she was going to draw dots, not pictures, “because dots are much easier to draw.” I expected, of course, to see her do essentially what the other children were doing, drawing one dot at a time as she counted from 1 to 30. Because Emma was as formal in her work as in her explanations, I wouldn’t have been surprised if those dots formed a neat row as far across the page as that row would fit, to be continued, if necessary, in a second row beneath it.

But that’s not what she did. Here is a retracing of Emma’s picture:

This orderly packaging of 30 is already a surprise, but the static picture doesn’t tell the whole story! Emma worked from top to bottom starting at the left, counting 1, 1, 1,   2, 2, 2,   3, 3, 3,  …  9, 9, 9,   10, 10, 10 as she drew. And then she stopped. She never said the word “thirty.” She drew ten columns of 3 instead of three rows of 10 (or the thirty individual dots that almost any other child might have drawn).

In many kindergarten classes it might seem remarkable enough for a child to know that three tens make 30, but most of the children in Emma’s class had become quite used to that idea. Calendar time, which always began with a song about calendars, had them counting the days of the year every school day with popsicle sticks, bundling ten days into a “ten” and bundling ten ten-bundles into a “hundred.” Using that, they named the current day—today was 167. They started with the “hundred,” successively added “tens” one by one, and then added each of the 1s, naming the results as they worked. These children had also counted money, including adding up the value of a few dimes. So nearly all of the children in Emma’s class knew, or could quickly figure out, that three tens make 30. They had plenty of classroom experiences that would also give them a chance to verify that counting by ones and counting by tens gave the same result. (Well, mostly. For a young child, counting by ones is so prone to error that counting by ones doesn’t always give the same answer!)

Emma, like the others, well understood this structure of multiple tens, but in her drawing she produced a different structure.

While children in this kindergarten had built and rehearsed the idea that three 10s make 30, they had no explicit experience in school to show that ten 3s would also make 30. I have no idea why Emma counted 30 dots that way, but she did have that idea so that’s how she drew it.

Could it be that this was just a stray multiplication fact that she gained from a sibling or parent? Possibly, but what was far more striking was the structure Emma used in her picture. That, too, might have been the result of some (home) teaching, but young children are often not able even to copy such a structure when they have it directly in front of them, let alone produce it from a mental model. Shown a 4 × 6 array

and given a partially-filled-in frame to complete by copying the model

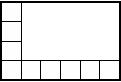
many young children will add squares to the empty frame without fully filling it in. Even those who fill it with squares may do so without using, or apparently even noticing, the row-column structure that assures exactly four rows of six squares, or, equivalently, six columns of four squares (see Goldenberg and Clements, 2014).

Though we don’t know what Emma may have learned outside of school, Emma’s work clearly shows more than a memorized fact. It shows her ability to visualize the structure, and her ability to predict its full form before drawing it, so that she could stop spontaneously at “10, 10, 10.”

Emma’s organizational plan is still barely discernible even in the static picture. Had she drawn horizontally, we might have expected each row to be fairly straight and the columns to be ragged. But her columns are straight. Her top row is straight, too, because she began each new column at roughly the same height as the last. Slightly uneven spacing within each column left the bottom row ragged.

But that plan is only barely discernible from the static picture. I was lucky to have been there to watch her draw that picture. (“Thank you for watching so patiently,” Emma said.) But observing was my only job there. When you are the teacher in charge, it’s way harder to free yourself to watch so closely; a lot of children are in your charge and even with an assistant, the pushes and pulls to attend to the children actually compete with attending closely.

As I noted, attending to the mathematical structures that children build helps us nurture their mathematical thinking. Herein lies an administrative puzzle. On the surface, Emma’s work is just another correct answer. Beneath the surface, we see mathematical thinking that is quite special. How can we run a school in a way that gives teachers the time and support to watch and listen actively and to recognize, understand, and help children build on the underlying mathematical ideas?